Computational Learning Theory: Mastering AI Learning

Computational Learning Theory (CLT) stands as a cornerstone in the realm of artificial intelligence (AI), providing a mathematical foundation for understanding how machines learn from data. This theoretical framework not only offers insights into the mechanisms behind learning algorithms but also delineates the boundaries of what can be learned and how efficiently it can be achieved. This introduction delves into the definition of computational learning theory, its significance, and its profound impact on the AI field.

1. Introduction: Unveiling Computational Learning Theory

Defining Computational Learning Theory

CLT is a branch of AI focused on creating and analyzing algorithms that can learn and make predictions. It combines computer science, statistics, and math to systematically study the learning process. CLT addresses important questions like:

How much data does an algorithm need to learn something?
What makes some tasks easy or hard for machines to learn?
How does the difficulty of a task affect the performance of the algorithm?

Significance and Impact in AI

CLT is important because it provides guarantees about how well learning algorithms perform. By understanding when and how algorithms can learn effectively, researchers can create better and more efficient AI systems. CLT helps:

Guide Machine Learning Development: It identifies trade-offs between accuracy, complexity, and the amount of training data needed, which is crucial for developing practical models.
Bridge Theory and Practice: It connects theoretical ideas with real-world applications, ensuring AI systems are based on solid principles.
Advance AI Research: It poses challenging questions and problems, pushing the boundaries of what we know about machine learning.

Computational Learning Theory is essential for advancing AI. It helps us understand the principles behind machine learning algorithms and shapes AI research and development. The next sections will explore the foundations of CLT, delve into the analysis of algorithms, examine practical applications, and discuss the challenges and future directions in this fascinating field..

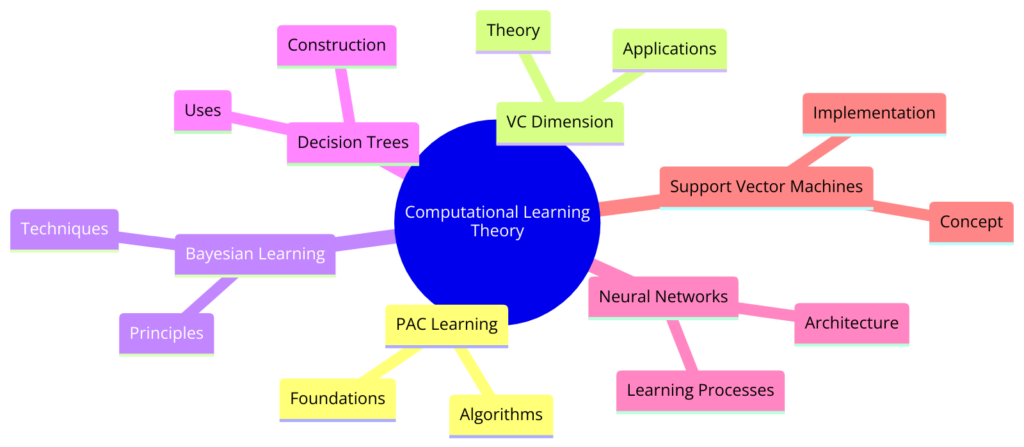
2. Foundations of Computational Learning Theory

CLT provides a framework for understanding how machine learning algorithms work and what they can do. By establishing a solid mathematical foundation, CLT offers insights into the efficiency, reliability, and limitations of learning processes. This section will explore the basic concepts and principles of CLT and introduce key theoretical models like Probably Approximately Correct (PAC) learning.

Basic Concepts and Principles

At the core of CLT are several key concepts:

Concept Classes and Hypothesis Spaces: CLT studies all possible concepts (or functions) a learning algorithm might need to learn and the set of hypotheses it can use to approximate these concepts.
Learning Models: These describe how learning happens, including where the data comes from and what needs to be learned.
Sample Complexity: This is the number of training examples needed for a learning algorithm to successfully learn a concept with a specified level of accuracy and confidence.
Computational Complexity: CLT also considers the time and memory needed for learning and how these resources scale with the size of the problem.

Overview of Key Theoretical Models

One of the main models in CLT is the Probably Approximately Correct (PAC) learning framework, introduced by Leslie Valiant in 1984. PAC learning provides a formal way to define learning from examples.

PAC Learning: This model defines learning as the ability of an algorithm to find a hypothesis that is close to the true concept with high probability, given enough examples. It addresses both accuracy and confidence in learning.
VC Dimension: The Vapnik-Chervonenkis (VC) dimension measures the capacity of a hypothesis space to fit data. It helps predict a model’s ability to generalize to unseen data, balancing model complexity and learning ability.
No Free Lunch Theorems: These theorems state that no learning algorithm is best for all possible tasks. The effectiveness of an algorithm depends on how well its assumptions match the specific learning problem.

The foundations of Computational Learning Theory are crucial for understanding machine learning. By defining the theoretical underpinnings of learning algorithms, CLT guides the development of more effective and reliable AI systems. As we explore the algorithms and their analysis within this framework, the importance of CLT in connecting theory and practice will become clearer.

3. Algorithms and Their Analysis in Computational Learning Theory

CLT provides a framework for analyzing learning algorithms, helping us understand their performance and limitations. This section will dive into how CLT categorizes and evaluates different algorithms, focusing on their performance and inherent limitations.

In-depth Look at Learning Algorithms

CLT categorizes algorithms based on their learning models, including supervised, unsupervised, and reinforcement learning. Each model has unique challenges and theoretical considerations.

Sample Complexity: This measures how many examples an algorithm needs to learn a concept accurately.
Error Bounds: These bounds define the maximum error between the learned hypothesis and the true concept, essential for evaluating algorithm reliability.
Computational Efficiency: This considers how an algorithm’s running time and memory use scale with the size of the input data, fundamental for real-world applications.

Key Theoretical Insights

Several theoretical insights are central to the analysis of learning algorithms in CLT:

PAC Learnability: This framework helps determine whether a concept class can be learned to any desired accuracy and confidence level in polynomial time.
VC Dimension: This measures the capacity of a hypothesis space to fit various training samples, helping balance model complexity and generalization ability.
Bias-Variance Tradeoff: This principle describes the tension between an algorithm’s ability to capture relevant patterns (bias) and its sensitivity to training set fluctuations (variance).

Analysis of Algorithm Performance and Limitations

Theoretical analysis in CLT highlights the capabilities and limitations of algorithms. For example:

Sample Complexity and Error Bounds: Algorithms with low sample complexity and tight error bounds may face practical challenges due to computational inefficiencies.
No Free Lunch Theorems: These remind us that no single algorithm is best for all tasks, emphasizing the need to select algorithms that match the specific problem.

Analyzing learning algorithms within the CLT framework provides essential insights into machine learning. By establishing performance bounds and identifying successful learning conditions, CLT guides the development of effective and efficient algorithms. As machine learning advances, the principles from CLT remain crucial for evaluating new algorithms and ensuring their robustness.

4. Applications in Machine Learning: Informing Practice with Theory

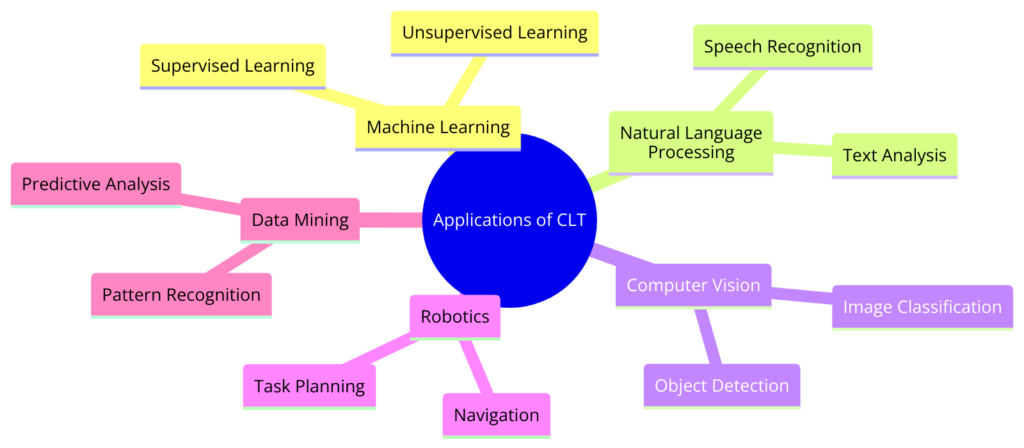
CLT provides a theoretical framework that informs practical applications in machine learning (ML). By bridging theory and practice, CLT enhances the development and implementation of ML models, ensuring they are efficient and effective. This section explores how CLT influences ML practices and showcases examples of theory-driven applications.

Informing Machine Learning Practices

Insights from CLT guide the practical application of ML algorithms in several key areas:

Model Selection and Complexity Management: CLT concepts like PAC learning and VC dimension help practitioners balance model complexity and generalization ability.
Performance Evaluation and Error Estimation: Theoretical bounds on error rates and sample complexity provide benchmarks for evaluating algorithm performance.
Algorithm Design and Optimization: Understanding the theoretical foundations of learning algorithms aids in designing more robust and efficient algorithms.

Examples of Theory-Driven Machine Learning Applications

Support Vector Machines (SVMs): Developed based on theoretical insights into margin maximization, SVMs are powerful tools for classification tasks with high-dimensional data.
Boosting Algorithms: Grounded in CLT principles, boosting algorithms like AdaBoost iteratively improve performance by focusing on difficult-to-classify instances.
Deep Learning and Neural Networks: While often seen as black boxes, CLT helps shed light on the learning dynamics of deep neural networks, guiding the design of architectures that capture complex patterns.

Bridging Theory and Practice

The interaction between CLT insights and practical ML challenges is dynamic and reciprocal. Theoretical models provide guidelines for practical algorithm design, while real-world challenges inspire new theoretical questions and models.

Computational Learning Theory’s influence on ML practices underscores the importance of a strong theoretical foundation. By informing model selection, performance evaluation, and algorithm design, CLT enhances the efficacy and reliability of ML applications. As AI evolves, the interplay between theory and practice will remain pivotal, guiding the development of sophisticated, efficient, and impactful ML solutions.

5. Challenges and Limitations in Computational Learning Theory

Despite its contributions, CLT faces challenges and limitations, particularly in bridging theoretical models and real-world applications. This section examines these challenges and limitations, highlighting the complexities of applying theoretical insights to practical ML tasks.

Practical Challenges in Applying CLT

Complexity of Real-World Data: Many CLT models assume idealized conditions that may not fully capture the complexity and noise in real-world data.
Scalability: Some theoretical models and algorithms may not scale efficiently to the vast amounts of data typically encountered in modern ML applications.
Model Assumptions: CLT often relies on specific assumptions about data distributions or learning environments that may not hold true in practice.

Theoretical Limitations of CLT

Limits of Learnability: While CLT helps us understand what can be learned and how efficiently, it also delineates the boundaries of learnability.
No Free Lunch Theorems: These theorems assert that no single learning algorithm can perform optimally across all tasks, emphasizing the need for task-specific algorithm design.
Generalization to Novel Tasks: Generalizing learned knowledge to entirely novel tasks or significantly different distributions remains a challenge for computational models.

Bridging Theory and Practice

Addressing the gap between theoretical models and practical application involves several strategies:

Developing More Flexible Models: Creating adaptable theoretical models that better capture real-world data complexities.
Enhanced Data Representation and Preprocessing: Improving data representation and preprocessing techniques to align with practical data characteristics.
Interdisciplinary Collaboration: Encouraging collaborations between theorists and practitioners to develop algorithms that are theoretically sound and practically viable.

The challenges and limitations in CLT highlight the tension between theoretical elegance and practical applicability. Translating CLT insights into effective real-world applications requires ongoing research and innovation. Addressing these challenges will be crucial for advancing machine learning and AI.

6. Emerging Trends and Future Directions in Computational Learning Theory

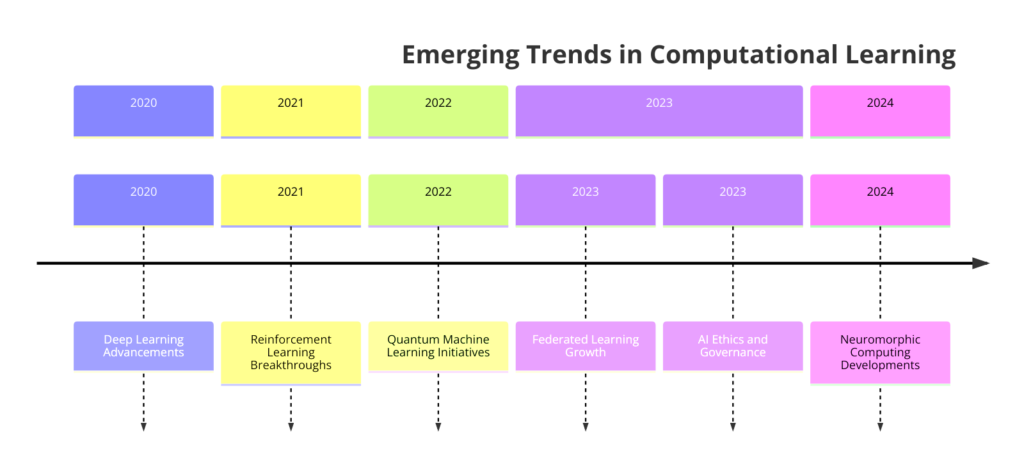
CLT continues to migrate in new research areas and theoretical advancements shaping the future of AI and ML. These developments promise to address current limitations, offer deeper insights, and open up novel applications. This section explores emerging trends and future directions in CLT and their impact on AI development.

Exploration of New Research Areas

Learning with Less Supervision: Models that require less human supervision, such as semi-supervised, unsupervised, and self-supervised learning, are gaining prominence.
Robustness and Generalization: Developing algorithms that are robust to data distribution shifts and adversarial attacks is a growing focus.
Interpretable and Explainable AI: As AI systems become more prevalent, the need for transparency and interpretability grows.
Fairness and Bias: Addressing bias and ensuring fairness in ML models are critical concerns.

Theoretical Advancements

Beyond PAC Learning: Researchers are exploring models that can adapt to changing data distributions and learn from interactive processes.
Quantum Machine Learning: Combining quantum computing with CLT opens new avenues for exploring efficient learning algorithms.
Neuro-Symbolic Learning: Combining neural networks with symbolic reasoning aims to bridge the gap between low-level perception and high-level cognition.

Predictions for the Impact on Future AI Developments

Advancements in CLT will influence the trajectory of AI and ML, enabling more advanced, reliable, and equitable systems. Exploring new paradigms like quantum ML and neuro-symbolic models hints at a future where AI can more closely mimic human-like reasoning and adaptability.

The future of CLT is vibrant and promising, with emerging trends and theoretical advancements poised to redefine AI and ML. Encouraging ongoing research and application in this field is essential for fostering innovation and ensuring AI development remains grounded in robust theoretical foundations.

7. Conclusion: The Integral Role of Computational Learning Theory in AI

CLT is a crucial field within AI, providing essential theoretical underpinnings that guide and inform the development of learning algorithms.

This concluding section reflects on the importance of CLT in AI and emphasizes the need for ongoing research to push the boundaries of machine learning.

The Importance of Computational Learning Theory

CLT offers a framework for assessing the capabilities and limitations of learning algorithms, addressing fundamental questions about learnability, efficiency, and complexity.

It bridges theoretical insights and practical applications, ensuring AI advances are both innovative and grounded in solid principles.

Encouraging Ongoing Research and Application

The dynamic nature of AI and ML requires continuous exploration and innovation in CLT.

Emerging areas like quantum ML and neuro-symbolic models represent new frontiers where CLT can provide guidance.

The ethical implications of AI also underscore the need for theoretical foundations to address issues like fairness, bias, privacy, and security.

Computational Learning Theory is essential for the progress and integrity of AI.

Its principles and models illuminate the path to advanced learning algorithms and ensure these technologies are developed with a deep understanding of their theoretical capabilities and limitations.

The continued integration of CLT into AI research and development will be paramount for unleashing the full potential of machine learning, fostering innovations that are transformative, ethical, and impactful.

Encouraging ongoing research in CLT and its application across diverse AI domains is a critical endeavor for the global AI community.

FAQ & Answers

1. What is Computational Learning Theory?

Computational learning theory is a subfield of AI focusing on the design and analysis of machine learning algorithms, based on mathematical and statistical principles.

2. How does Computational Learning Theory apply to AI?

It provides a theoretical foundation for understanding how and why learning algorithms work, guiding the development of more efficient and effective AI systems.

Quizzes

Quiz 1: “Theory to Application”

Instructions: Match each computational learning concept with the correct application in AI. Some applications might use more than one concept.

Concepts:

Supervised Learning
Unsupervised Learning
Reinforcement Learning
Decision Trees
Neural Networks
Genetic Algorithms
Support Vector Machines (SVM)

Applications:

A. Predicting stock market trends based on historical data.

B. Optimizing the strategy of a chess-playing AI.

C. Clustering customers based on shopping behavior without predefined categories.

D. Recognizing faces in images.

E. Routing packets in a computer network to minimize travel time and avoid congestion.

F. Identifying fraudulent transactions from a dataset of credit card transactions.

G. Generating new designs for automotive parts that optimize for both strength and material efficiency.

Answers:

A, F – Supervised Learning is used when we have labeled data to predict outcomes or categorize data.
C – Unsupervised Learning is used to find hidden patterns or intrinsic structures in input data without labeled responses.
B – Reinforcement Learning involves learning to make decisions by taking actions in an environment to achieve some objectives.
F – Decision Trees are a method used in various applications, including fraud detection, by learning decision rules inferred from the data features.
D – Neural Networks are widely used in image recognition and can learn complex patterns for tasks like face recognition.
G – Genetic Algorithms are used in optimization problems, such as designing parts to meet specific criteria by simulating the process of natural selection.
A – Support Vector Machines (SVM) can be used for classification or regression challenges, such as predicting stock market trends by finding the hyperplane that best divides a set of input features into two classes.

Quiz 2: “Learning Theory Fundamentals”

Instructions: Choose the best answer for each question to test your understanding of basic principles in computational learning theory.

What is the primary goal of computational learning theory?
- A) To create algorithms that require minimal computational resources
- B) To understand the fundamental principles that underlie the learning process
- C) To develop more efficient data storage techniques
- D) To improve the speed of computer processors
Which of the following best describes the concept of overfitting?
- A) When a model performs well on the training data but poorly on unseen data
- B) The process of selecting the best model based on its performance on a validation set
- C) A technique used to speed up algorithm performance
- D) Reducing the dimensionality of the input data
In the context of supervised learning, what is a ‘label’?
- A) A unique identifier for each data point
- B) The outcome or category assigned to each data point
- C) The algorithm used to train the model
- D) A measure of the model’s accuracy
What does the term ‘generalization’ refer to in machine learning?
- A) The ability of a model to perform well on previously unseen data
- B) The process of simplifying an algorithm to run faster
- C) Reducing the size of the training dataset
- D) Combining several models to improve performance
Which learning paradigm involves the algorithm making decisions based on a reward system?
- A) Supervised Learning
- B) Unsupervised Learning
- C) Reinforcement Learning
- D) Semi-supervised Learning